Reflection and Transmission Amplitudes

When a wave strikes an interface between two materials with differing physical properties, some of the wave energy will be reflected and the rest will be transmitted through or along the interface. All of the processing and interpretation methods we will discuss will assume that a seismic wave striking the interface between materials of differing physical properties can be approximated as a plane wave. We define a new quantity called acoustic impedance as \(Z = \rho V\), the product of density and velocity. The velocity in question could be for either P or S waves.

Let us first consider waves striking an interface at normal incidence, i.e. with the direction of propagation perpendicular to the interface. The relative amplitudes of the reflected and transmitted waves will depend on the acoustic impedances of the two materials. Let \(A_0\), \(A_1\) and \(A_2\) be the amplitudes of the incident, reflected, and transmitted waves, respectively. The ratios of \(A_1\) and \(A_2\) to \(A_0\) are given by the reflection and transmission coefficients:

Reflection Coefficient:

\[R = \frac{A_1}{A_0} = \frac{Z_2 - Z_1}{Z_2 + Z_1} \qquad -1 \le R \le 1\]

Transmission Coefficient:

\[T = \frac{A_2}{A_0} = \frac{2 Z_1}{Z_2 + Z_1} \qquad 0 \le T \le 2\]

The following figure shows the progression of amplitude as a vertical seismic wave propagates through the earth.

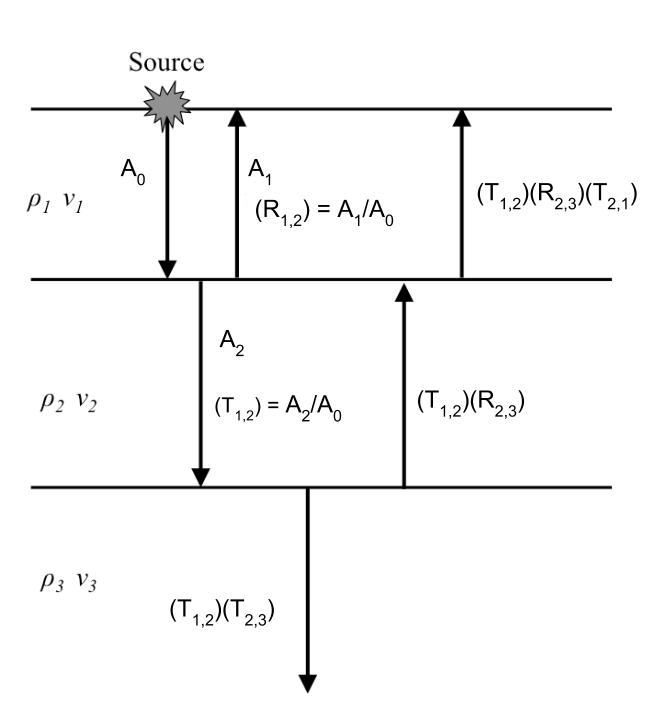
Displacement of the earth from equilibrium position must be continuous across any interface. This guarantees that \(A_0 = A_1 + A_2\). We make note of the values of \(R\) and \(Z\) in some important special cases:

1. If \(Z_1 = Z_2\): \(R = 0\), \(T = 1\)

2. If \(Z_1 >> Z_2\): \(R = -1\), \(T = 2\). The value \(R = -1\) means that the pulse will be reflected with a polarity change, for example at the rock-air interface, with an upward traveling wave.

3. If \(Z_2 >> Z_1\) \(R = 1\), \(T = 0\) (wave travelling down through the air and hitting the air earth interface).

We can illustrate scenarios two and three using the example of a wave propagating on a string. A string with a free end represents scenario two and a string with a fixed end represents scenario three. These are illustrated in the following video

You can explore the concept further using an interactive web app here.

Remark: Large amplitudes of the transmitted wave are sometimes counter- intuitive. However, the energy transported in an acoustic wave of frequency \(f\) traveling at velocity \(V\) is

\[\text{Energy} = \frac{1}{2} \rho V (2\pi f)^2 A^2 \propto ZA^2\]

The symbol \(\propto\) indicates “proportional to”. As a consequence, even though there is an enhanced amplitude of a transmitted wave in certain situations, there is still conservation of energy. The ratio of incoming to reflected energy is \(E_R\) and the ratio of incoming to transmitted energy is \(E_T\). In terms of the impedances on either side of the interface, The energy ratios are

\[E_R = Z_1 \left( \frac{Z_2 - Z_1}{Z_2 + Z_1} \right)^2 A_0^2\]

\[E_T = Z_2 \frac{4 Z_1 Z_1}{(Z_2 + Z_1 )^2} A_0^2\]

\[E_R + E_T = Z_1 A_0^2\]