Seismic Waves¶
Waves and Rays¶
A wave is a representation of the propagation of energy. In the case of seismic waves, energy is propagated through small displacements of the earth away from equilibrium. Energy propagates away from seismic source with a distinct pattern. Most seismic sources can be approximated spatially as point sources. In a uniform medium, energy propagates away from a point source in an expanding spherical pattern, much like ripples on a pond that’s been disturbed. The figure below shows a snapshot of waves on a pond. Notice how each ring forms a coherent surface where the water is disturbed from equilibrium by an equal amount. These rings propagate outward in time, in a coherent manner.

Fig. 47 Image reproduced with permission from The website of the Gemini Observatory. The original can be found here.¶
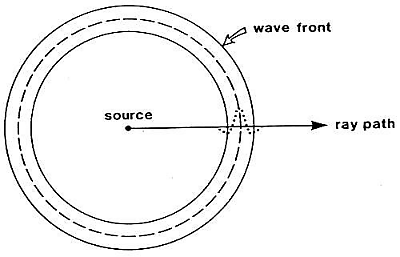
A wavefront indicates the set of locations at which the phase of the wave has the same value. To continue with the pond example, visualize the peaks (or troughs) of water ripples after a rock has been thrown in. The direction of propagation of the energy is normal to the wavefront. Seismic rays are imaginary lines perpendicular to the wavefront that indicate the path along which the wavefront is traveling. Rays are not physical entities. They exist only to illustrate where the energy travels. It is important to remark here that the arrival of energy at a geophone is not a point event. The energy is spread in space and time. Note how the peaks and troughs of the waves on the pond have widths, which remains constant as they propagate. Similarly, seismic energy will arrive at a geophone as a pulse of energy with some shape and width, not as a spike occurring a single instance in time. This pulse of energy is called a wavelet.
Lets illustrate the connection between wavefronts and rays using a seismic example. Have a look at the following animation.
The color represents a propagating wavefront due to a point source and the arrows are rays showing the direction of propagation. Note how the rays represent how the wavefront is bent when it hits the interface between two layers in the earth. They are always normal to the wavefront.
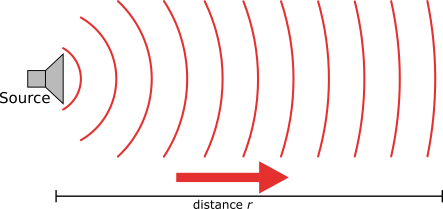
It is common in seismic processing and interpretation to represent waves as plane waves, that is, waves whose wavefronts are straight lines rather than circles. The wavefronts maintain a circular shape when propagating in a uniform medium but as they expand away from the source the circles get larger and larger, to the point where the curvature is negligible and they can be approximated as planes. this is illustrated in the figure below
Attenuation¶
The amplitude of seismic waves falls off with distance from the source. There are two primary reasons:
Geometrical spreading - that is, energy falls off as \(1/r^2\) and hence the amplitude falls of as \(1/r\).
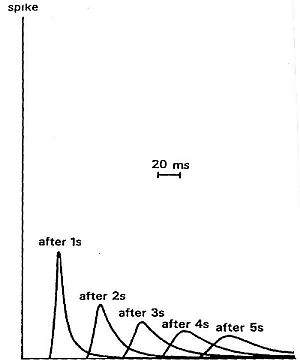
Earth materials are not perfectly elastic. Some frictional heating occurs as the waves propagate through the earth. This is often described as “absorption” and the absorption coefficient expresses the proportion of energy lost as the wave travels a distance of one wavelength. The figure here shows the progressive change of shape of an original spike pulse during its propagation through the ground due to the effects of absorption (after Anstey 1977.) The spike’s shape changes as well as experiencing reduced amplitude. This is because the different frequencies making up the pulse decay at different rates - in fact, higher frequencies decay more rapidly than lower frequencies. This is easily observed on earthquake signals that have been recorded at different locations. As noted above in the context of surface waves, such frequency dependent behavior is called dispersion.