Seismic Velocity

Rocks and other materials can be characterized by their elastic properties. However, seismic velocities represent a more practical set of physical properties for seismic methods. Seismic velocities define the speed at which various elastic deformations propagate through materials. And as we will see, seismic velocities for a given material can be expressed explicitly in terms of its elastic properties.

Body Waves

In seismology, there are two fundamental types of body waves: pressure waves (“P-waves”) and shear-waves (“S-waves”).

P-waves

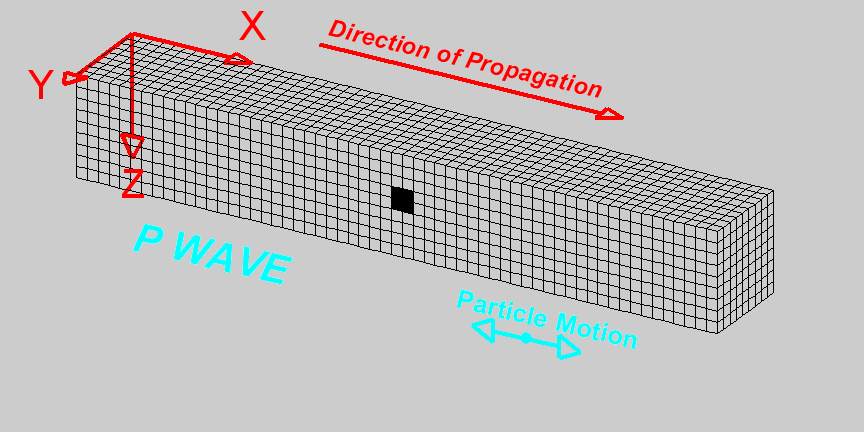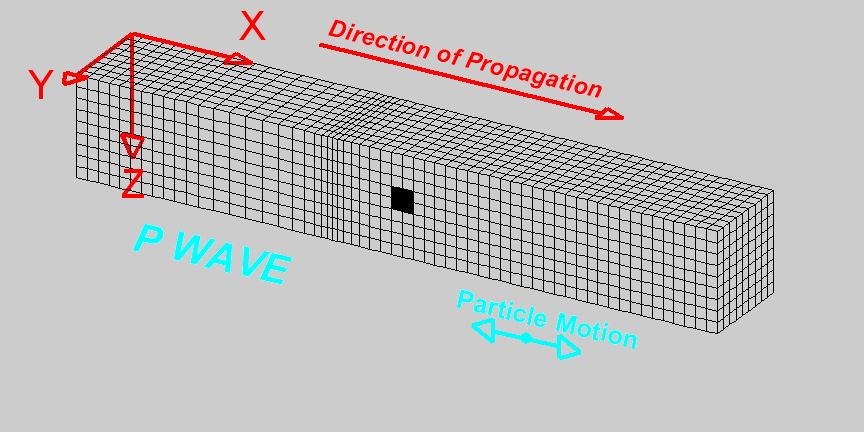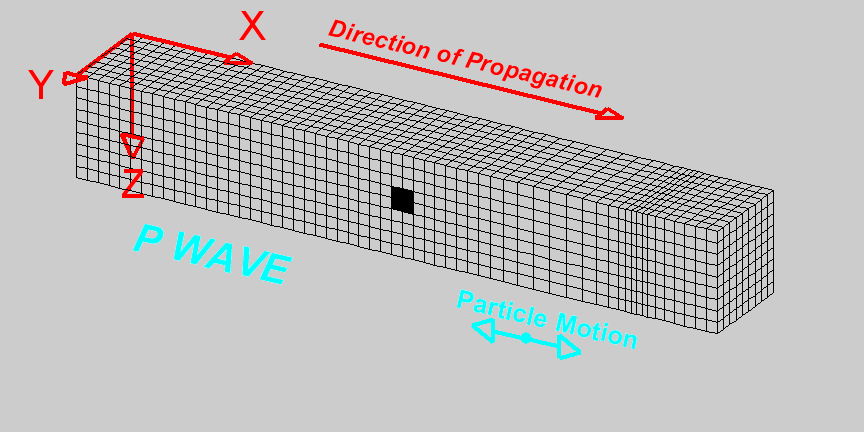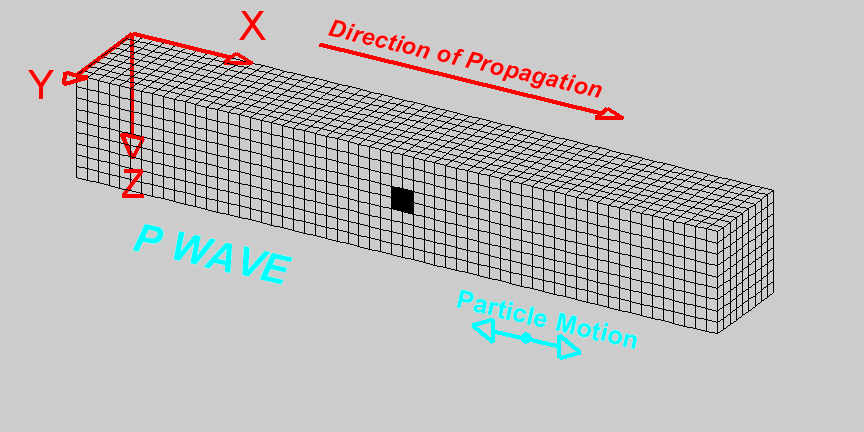
P-waves are compressional waves in which particle motion is in the direction of the wave propagation. The compression and extension of the medium, and the propagation of the wave, can be seen in the diagram on the right [1]. As we can see, cells change volume when they come in contact with the wave. The P-wave velocity is related to the elastic properties of the medium by the following expression:

\[v_p = \sqrt{\frac{K+4/3\mu}{\rho}}\]

where \(K\) is the bulk modulus, \(\mu\) is the shear modulus and \(\rho\) is the density.

S-waves

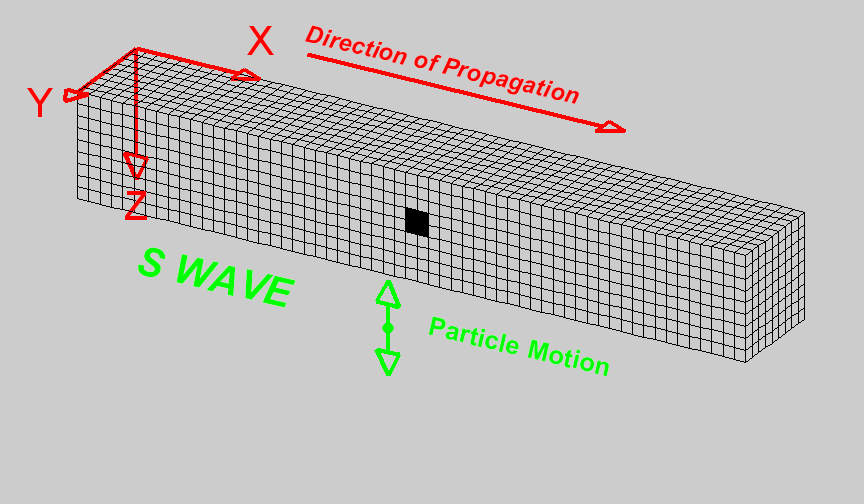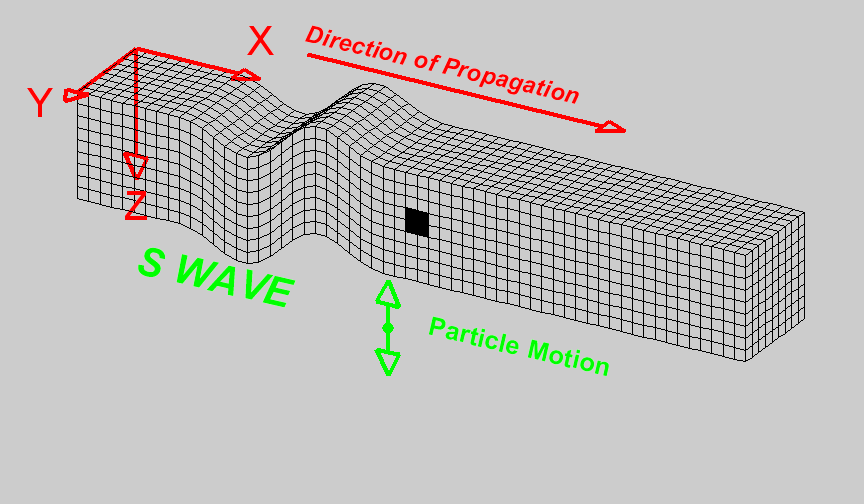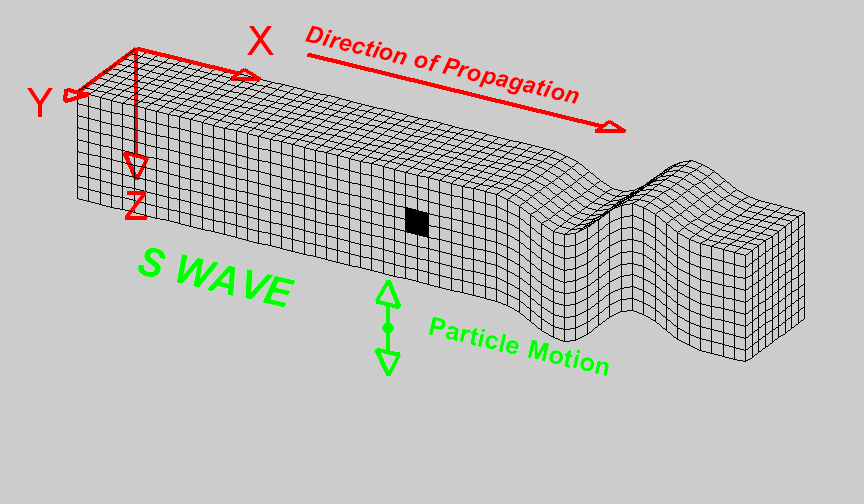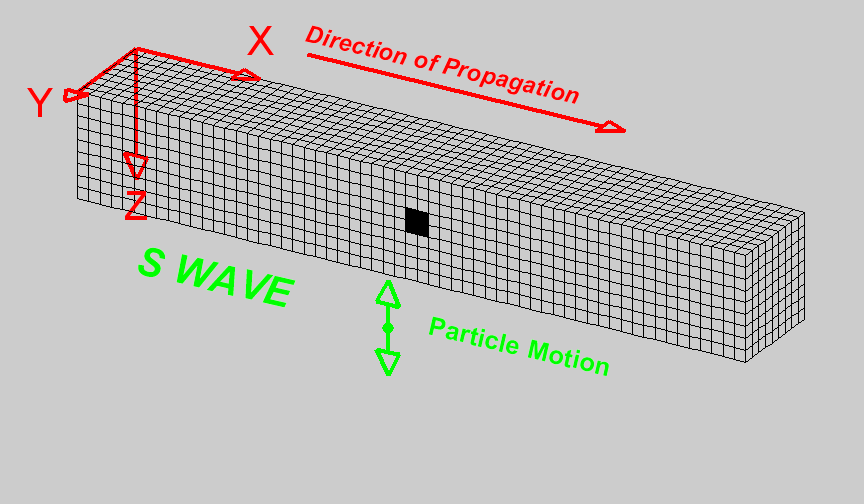
S-waves are shear waves in which the particle motion is perpendicular to the direction of wave propagation. The shearing action and the propagation of the wave can be seen in the diagram on the right [1]. Cells change shape but do not change volume when they come in contact with the wave. When there is a reference interface, such as the surface of the earth, S-waves are labelled as SH (horizontal shear) and/or SV (vertical shear). This is used to indicate the direction of particle motion with respect to the surface. In isotropic media, SH and SV waves travel at the same speed. The S-wave velocity can be related to the elastic properties of the medium by the following expression:

\[v_s = \sqrt{\frac{\mu}{\rho}}\]

S waves propagate through materials more slowly than P waves. In addition, S waves cannot propagate through fluids, as fluids do support shear particle motion.

Surface Waves

In seismology, there are two fundamental types of surface waves: Rayleigh waves and Love waves.

Rayleigh waves

Rayleigh waves are surface waves in which particle motion is elliptic. The particle motion which defines Rayleigh waves can be seen in the diagram on the right [1]. In Rayleigh waves, elliptic particle motion can be prograde (in the same direction as the propagating wave) or retrograde (in the opposite direction as the propagating wave). The amplitude of the elliptic motion decreases with depth. As a general rule, Rayleigh waves at the surface of the Earth have a propagation speed which is 90 % the speed of shear waves, thus:

\[v_R = 0.9 \, v_s\]

Love waves

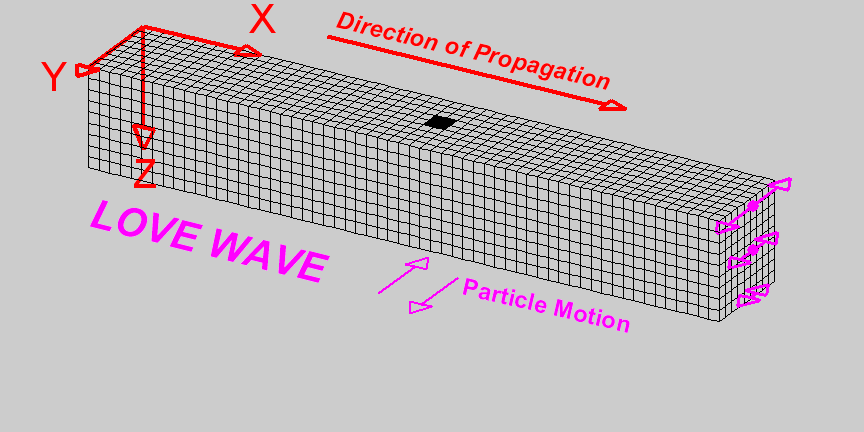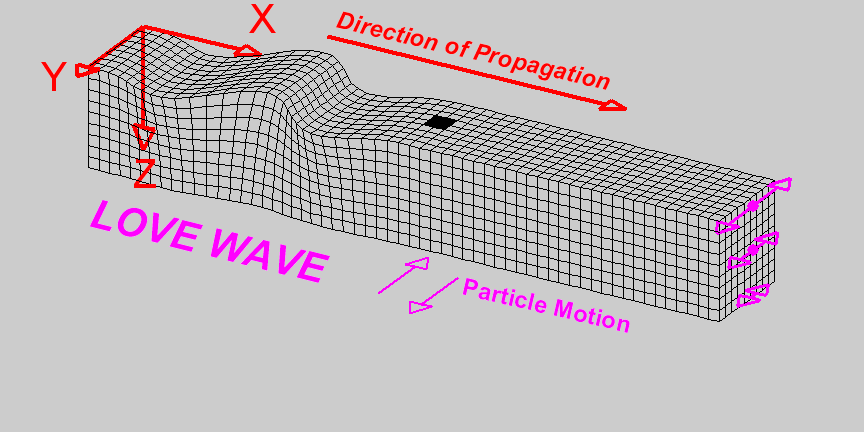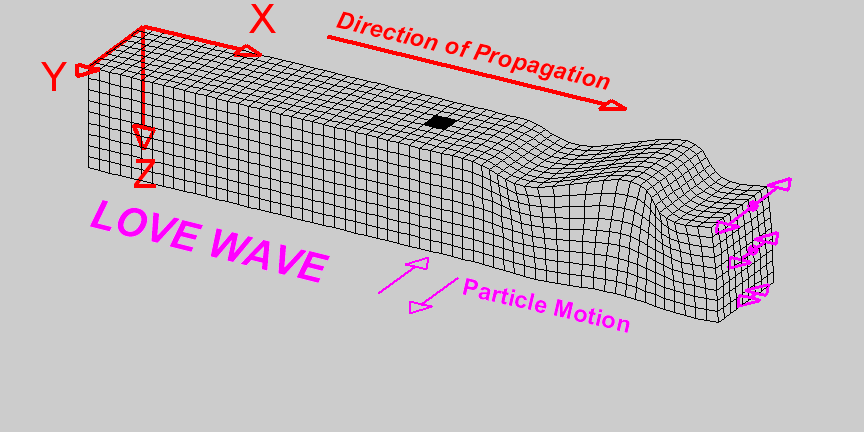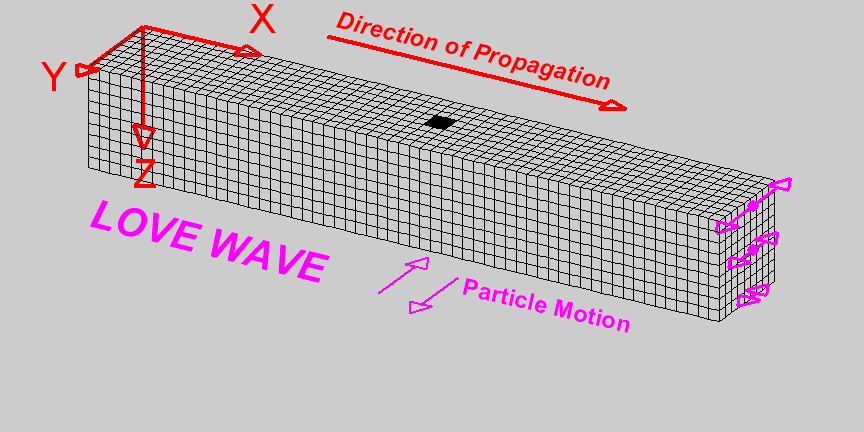
Love waves are surface waves in which particle motion is parallel to the Earth’s surface and perpendicular to the direction of wave propagation. The particle motion which defines Love waves can be seen in the diagram on the right [1]. The amplitude of lateral motion which describes Love waves decreases with depth. Love waves travel faster than Rayleigh waves but do not travel as fast as P or S waves. Thus Love waves have a propagation speed of:

\[0.9 \, v_s < v_L < v_s\]

Symbols used to define P-wave and S-wave velocities, as well as the elastic properties on which they depend, are summarized in the following table:

Property	Symbol	Units
P-Wave Velocity	\(v_p\)	m/s or km/s
S-Wave Velocity	\(v_s\)	m/s or km/s
Bulk Modulus(Incompressibility)	\(K\)	Pa or GPa
Shear Modulus (Rigidity)	\(\mu\)	Pa or GPa
Density	\(\rho\)	kg/m \(\!^3\) or g/cm \(\!^3\)

P-Wave and S-Wave Velocity Measurements

Ultrasonic Elastic Wave Velocity Measurements

To measure the P-wave and S-wave velocities for a given rock, a core sample is taken. The core sample is then held in place between two piezometric transducers. Piezometric transducers contain materials which contract and expand in response to an applied voltage.

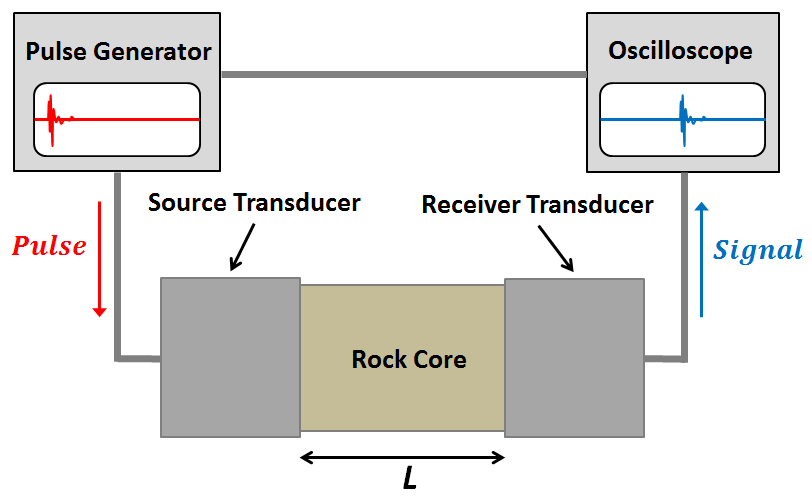
The measurement apparatus works by generating a short current pulse. As a result of the incoming current pulse, materials within the source transducer undergo elastic deformation. This elastic deformation is then transferred to the rock core where it propagates as elastic waves. On the other side of the rock, a receiver transducer registers the elastic waves and transforms the corresponding energy back into a current signal. This current signal is then measured by an oscilloscope.

Using the oscilloscope, we can determine the amount of time (\(\Delta t\)) it took for the elastic waves to propagate through the rock core. Given that we know the length of the rock core (\(L\)), the seismic velocity is given by:

\[V = \frac{L}{\Delta t}\]

In practice, the user may control whether they are measuring P-wave or S-wave velocities by specifying the direction of elastic deformation within the source transducer. Elastic deformation parallel to the length of the core results in P-wave velocity measurements, whereas elastic deformation perpendicular to the length of the core results in S-wave velocity measurements.

P-Wave and S-Wave Velocities in Common Rocks

P-waves and S-waves travel at different speeds depending on the media they are propagating through; P-waves travel faster than S-waves. P-waves are able to propagate through solids and fluids, however, S-waves can only propagate through solid materials. Given that there are so many factors which impact the velocity of seismic waves, it is impossible to assign a single value to a particular rock type. Therefore, the seismic velocities of rocks are generally defined over a range. The range of P-wave and S-wave velocities for common materials are shown below:

Material	P-wave (m/s)	S-wave (m/s)
Air	343	N/A
Water	1450 - 1500	N/A
Ice	3400 - 3800	1700 - 1900
Oil	1200 - 1250	N/A
Vegetal Soil	300 - 700	100 - 300
Dry Sands	400 - 1200	100 - 500
Wet Sands	1500 - 2000	400 - 600
Saturated Shales and Clays	1100 - 2500	200 - 800
Porous and Saturated Sandstones	2000 - 3500	800 - 1800
Marls	2000 - 3000	750 - 1500
Chalk	2300 - 2600	1100 - 1300
Coal	2200 - 2700	1000 - 1400
Salt	4500 - 5500	2500 - 3100
Anhydrites	4000 - 5500	2200 - 3100
Limestones	3500 - 6000	2000 - 3300
Dolomites	3500 - 6500	1900 - 3600
Granite	4500 - 6000	2500 - 3300
Basalt	5000 - 6000	2800 - 2400
Gneiss	4400 - 5200	2700 - 3200

Factors Impacting the Seismic Velocity

Given that P-wave and S-wave velocities both depend on the shear modulus and density of the material, many of the factors which impact the P-wave velocity will affect the S-wave velocity in a similar manner. Below are some of the factors which are known to affect the seismic velocities in materials.

Mineralogy and Structure

The mineralogy and structure of a rock determines its bulk modulus, shear modulus and density; which define the P-wave and S-wave velocities. In general, igneous, metamorphic, carbonate and anhydrite rocks have relatively large seismic velocities compared to soils and most sedimentary rocks. This is because the aforementioned rocks only deform under extreme compressional and shear stresses, and are therefore characterized by larger bulk and shear moduli. In sandstones and soils, clays have a tendency to present in load-bearing positions. As a result, seismic velocities are heavily influenced by clay content. Even in small abundances, clays have been shown to significantly reduce the seismic velocity by reducing the shear modulus.

Porosity

The most significant factor affecting seismic wave velocities is porosity. In the above table, we saw that seismic waves travel faster in solids than they do in fluids; with S-waves being unable to propagate through fluids. Thus as the porosity of a rock increases, both the P-wave and S-wave velocities will decrease. This is because seismic wave propagation becomes less efficient when forced through a fluid. Although it will not be explained here, the pore structure also plays an important role in reducing the efficiency of seismic wave propagation within rocks.

Pore Fluid and Saturation

Pore fluid determines the elastic properties of the pore space. Since P-wave velocity is larger in water and oil than it is in air, the P-wave velocity of a rock is less impacted by porosity if the pore-space is saturated. Additionally, the S-wave velocity has been shown to depend on the density of the pore fluid. As a result, P-wave and S-wave velocities increase as pore saturation increases. This can be described in a rudimentary manner using Wyllie’s equation:

\[V_{bulk} = \Bigg [ \frac{\phi}{V_{fluid}} + \frac{1-\phi}{V_{matrix}} \Bigg ]^{-1}\]

where \(0 \leq \phi \leq 1\) is the fractional % fluid saturation, \(V_{fluid}\) is the seismic velocity of the fluid, \(V_{matrix}\) is the seismic velocity of the solid material within the rock, and \(V_{bulk}\) is the bulk seismic velocity for the rock.

Lithification

Lithification describes the geological process in which unconsolidated sediments become consolidated through compaction and cementation. When subject to tectonic compression, or under the weight of overlying geological units, sediments and soils become compacted. This compaction reduces the pore-space which ultimately increases the P-wave and S-wave velocities. As a result, the seismic velocities of sedimentary units frequently increase with depth.

Cementation refers to chemical fluid processes in which pore space is replaced by a precipitate and mineral grains become fused to one another. Cementation increases the incompressibility and rigidity of the sedimentary rock, thus increasing its bulk and shear moduli. Ultimately, this process is responsible for increasing the seismic velocities.

Footnotes

[1] (1,2,3,4)

12. Braile, http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm, Copyright 2004-2010,